DOI: 10.1109/TMTT.2023.3297406   IEEEXplore: https://ieeexplore.ieee.org/document/10209380    

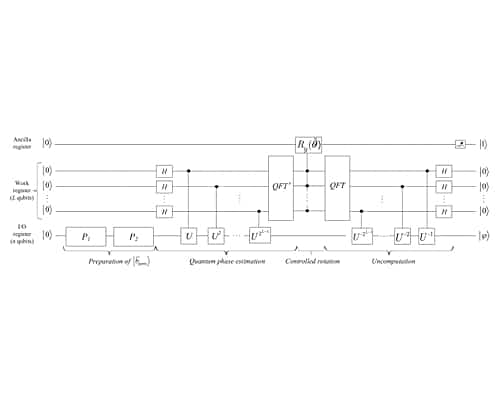
Quantum computer applying the Harrow-Hassidim-Lloyd (HHL) algorithm to solve finite element method (FEM) equations for electromagnetic (EM) problems with a minimum number of qubits.

Any

The number of gates necessary for quantum state preparation is reduced according to the sparsity pattern of the right-hand vectors of the finite element equation in the EM problem. A matrix preconditioner is applied to address the large condition number in the finite element matrix, modify the linear equations, and reduce the number of qubits required for computation.

The solution of large-scale EM problems

No criterion is presented for performance. Quantum computation to solve FEM equations for EM problems is anticipated to rapidly outperform classical computers for large-scale EM problems as hardware develops.