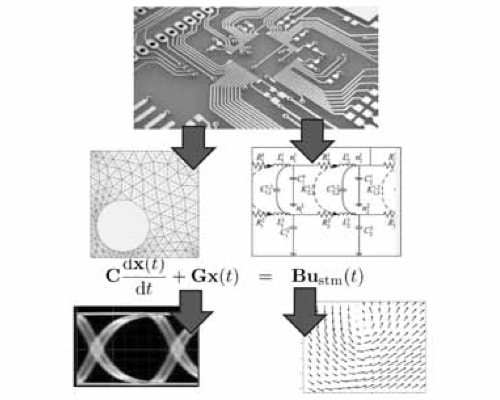
Modified Inversion of the Laplace Transform for Fast and Stable Time-Domain Simulation of Nonlinear Circuits
Abstract
DOI: 10.1109/TMTT.2025.3540771
IEEEXplore: https://ieeexplore.ieee.org/document/10900587
Device
Time domain nonlinear circuit simulation technique applying a modified numerical inversion of the Laplace transform technique.
Spectrum
Any
Novelty
Numerical inversion of the Laplace transform (NILT) creates a stable time-stepping scheme for circuit analysis and simulation in the time domain. Circuits are split into linear and nonlinear parts. Matching time domain derivatives at the interface is accomplished using NILT and rooted tree (RT) methods. An advanced NILT technique is applied that uses nth-order derivatives instead of zeroth-order derivatives to significantly improve simulation accuracy and efficiency.
Application
Computationally efficient nonlinear circuit analysis and simulation.
Performance
Compared to a reference trapezoidal rule (TR) analysis technique applied to two modified nodal analysis (MNA) sizes, NILT0 (zeroth-order) and NILT2 (2nd-order) analysis both significantly improved computational efficiency. Computational efficiency doubled for NILT2 analysis compared to the conventional NILT0 method.
For MNA size (K) = 3652, analysis was accomplished in 15 time steps for both NILT0 and NILT2 methods compared to 517 time steps for the TR reference. Computational speedup was 16x for NILT0 analysis and 31x for NILT2.
For K = 12171, analysis was accomplished in 16 time steps for both NILT0 and NILT2 methods compared to 517 time steps for the TR reference. Computational speedup was 69x for NILT0 analysis and 139x for NILT2.